엣코더 ABC #348의 E - Minimize Sum of Distance 에서 트리 DP, 그중에서도 전방향 트리(全方位木) DP를 쓴다고 해서 찾아봤습니다.
이 알고리즘은 일본 외에서는 Rerooting 이라고 불리며, 루트가 정해지지 않은 트리에서 조건에 맞는 루트를 구할 때 유용하게 사용할 수 있는 테크닉입니다. 한국에서는 트리에서의 다이나믹 프로그래밍 분류의 일종으로 취급되지만, 외국에서는 이름을 따 붙힐 정도로 경쟁적 프로그래밍에서 은근 자주 출제되는 알고리즘인 듯 합니다.
개념
트리 DFS
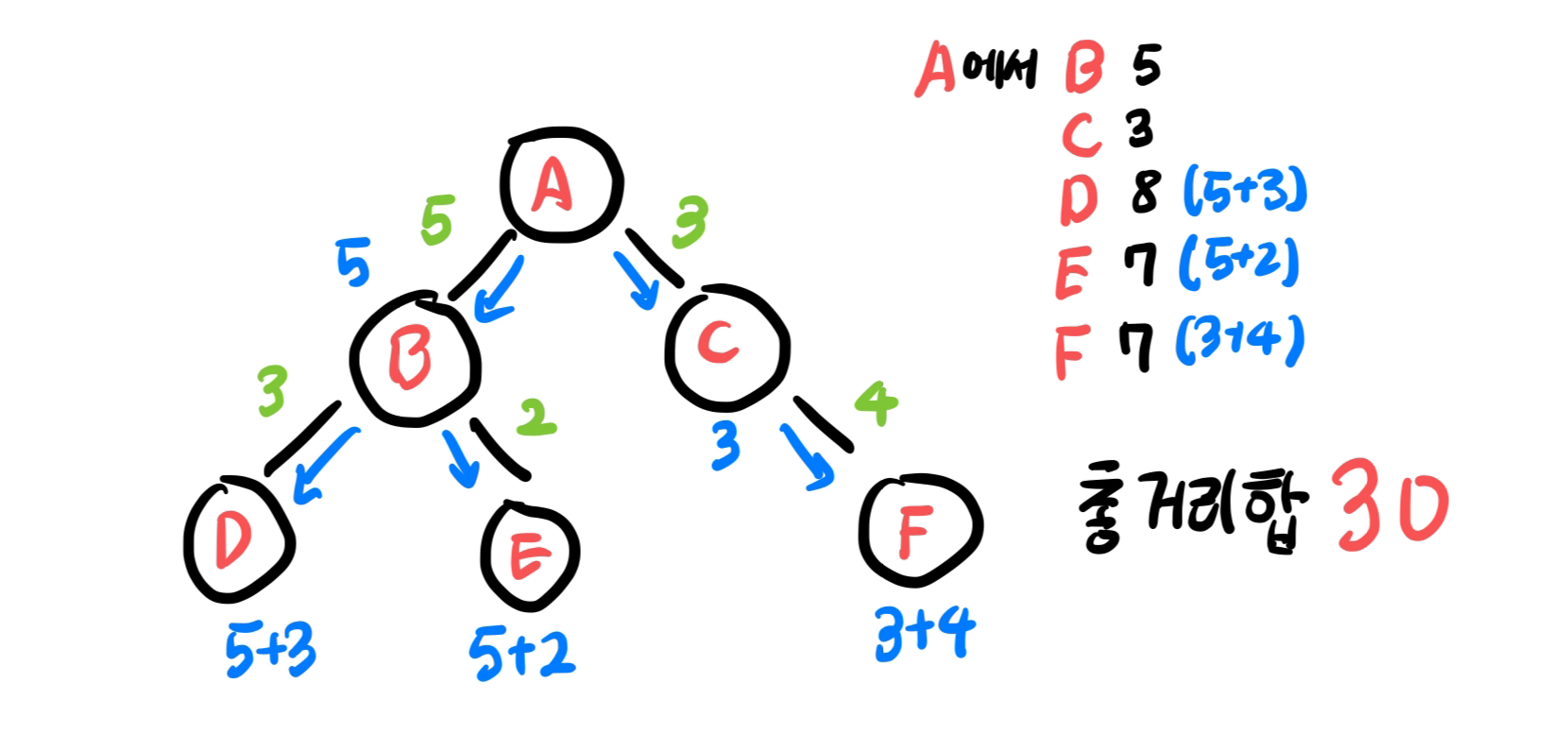
우선 특정 노드에 대해서 다른 노드까지 가는 간선 비용의 총합을 구하는 방법을 생각해 봅시다. 이는 DFS+DP를 통해 \(O(n)\)으로 구현할 수 있습니다.
리루팅
그렇다면 다른 노드까지 가는 간선 비용의 총합이 가장 작은 노드는 어떻게 구할 수 있을까요? 위에 설명한 트리 DFS를 노드의 개수만큼 사용하면 되겠지만, 그렇다면 \(O(n^2)\)이 소요되어 정점이 \(10^5\)개만 넘어가면 시간초과가 날 것입니다.
바로 이때 리루팅 테크닉을 사용합니다. DFS+DP트리의 루트를 옮기는 것은 \(O(1)\)에 가능하다는 것을 이용하는 테크닉입니다.
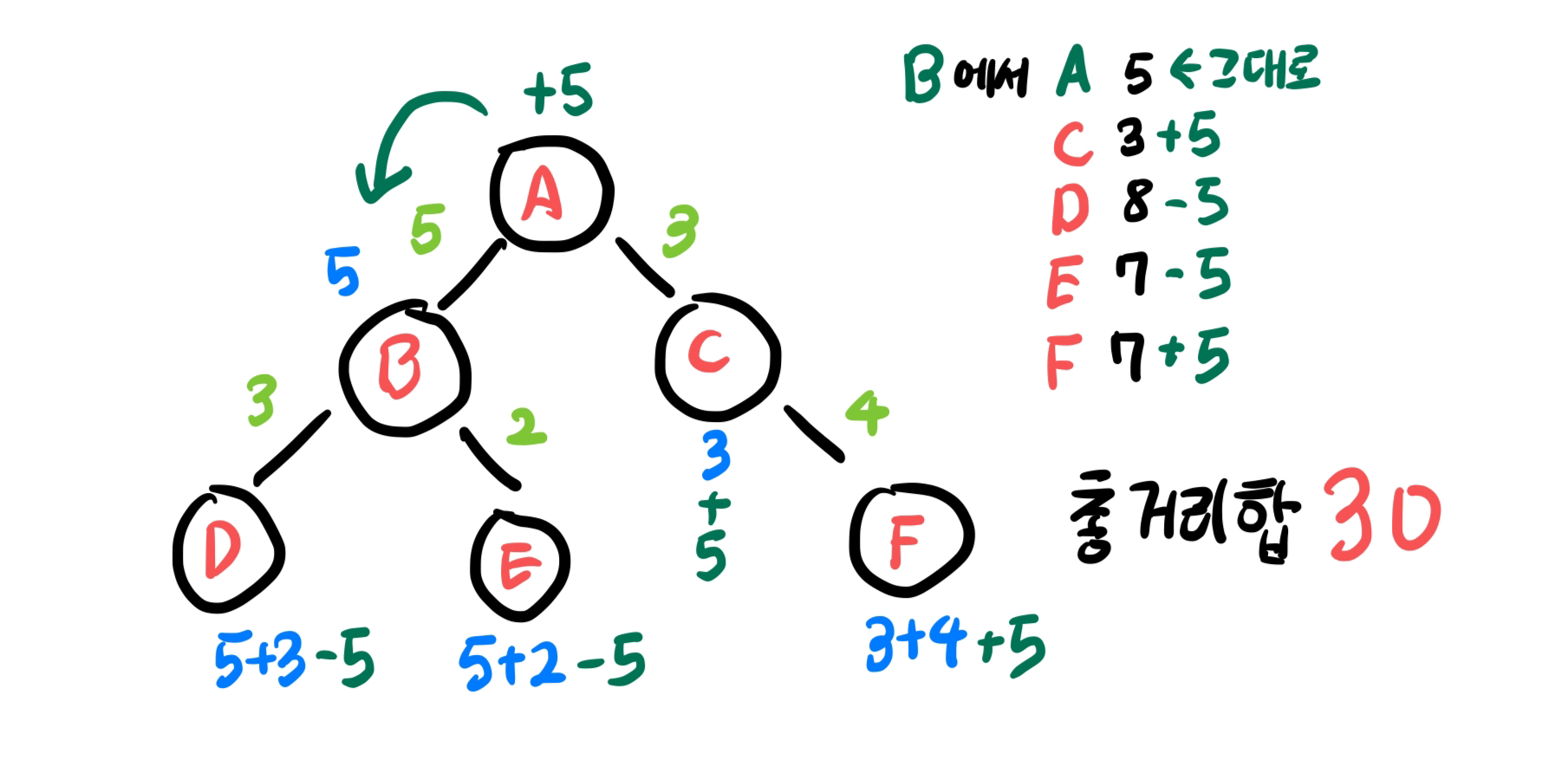
위 그림에서, A노드의 총 거리합인 30을 이용해서 B노드의 총 거리합을 구해봅시다. A노드와 그 너머에 있는 A(0), C(3), F(7) 노드의 거리는 A-B 간선의 비용 5만큼 증가해서, A(5), C(8), F(12)가 될 것이고, B노드와 그 아래에 있는 B(5), D(8), E(7) 노드의 거리는 A-B 간선의 비용 5만큼 감소해서 B(0), D(3), E(2)가 될 것입니다. A노드의 증가분과 B노드의 감소분은 서로 상쇄되니까
즉, (A의 총 거리합) - {(A노드 너머 노드 수) - (B노드 아래 노드 수)} * (A-B 간선의 비용)}이 B노드의 총 거리합이 되는 거죠.
이 방법을 이용해서 A노드의 총 거리합을 알 때, B노드의 총 거리합을 \(O(1)\)에 구할 수 있습니다.
이 테크닉을 루트를 옮기다고 생각하면 리루팅 테크닉이고, 양방향으로 검색하며 DFS를 돌린다고 생각하면 전방향트리 DP라는 이름이 됩니다. 알고리즘이 대부분 그렇듯 이름은 별로 중요하지 않습니다.
여기서 A노드 너머 노드 수와 B노드 아래 노드 수는 A의 총 거리합을 구하는 첫 DFS를 할 때, 서브노드의 개수를 함께 저장해두면 구할 수 있습니다. 위의 예시로 들면, A의 서브노드 개수 - B의 서브노드 개수가 A 너머의 노드 수가 되겠고, B의 서브노드 개수가 그대로 B노드 아래 노드 수가 되겠네요.
예제
BOJ 27730 : 견우와 직녀
위 예제를 그대로 적용할 수 있는 문제입니다. 트리 두 개에 대해서 시행하고, 양 쪽에서 거리합이 가장 작은 노드를 출력하면 됩니다.
BOJ 7812 : 중앙 트리
중앙 노드를 리루팅을 이용해 구한 다음, 다시 DFS를 돌려서 모든 노드에서의 거리를 출력하면 됩니다.
ABC#348 E
제가 리루팅 테크닉이라는 이름을 처음 알게 된 문제인데, 간선의 비용이 아닌 정점의 비용이 주어집니다.
즉, (해당 정점으로 가는데 필요한 간선 수) * (정점의 비용)이 간선의 비용이 됩니다.
이 문제는 정점의 비용 합 c[x]와 거리 합c[x]*d를 모두 기억하면서 해결하면 됩니다.
정리한 정해 코드는 아래와 같고, 해설은 에디토리얼이 있으니 참조해 주세요.
#include <bits/stdc++.h>
using namespace std;
#define llint long long int
int main() {
int n;
cin >> n;
vector<int> a(n - 1), b(n - 1);
vector<vector<int>> tree(n);
for (int i = 0; i < n - 1; i++) {
cin >> a[i] >> b[i];
a[i] -= 1;
b[i] -= 1;
tree[a[i]].push_back(b[i]);
tree[b[i]].push_back(a[i]);
}
vector<llint> c(n);
for (int i = 0; i < n; i++)
cin >> c[i];
//sum_c[i]는 루트를 i로 하는 트리에 대해 정점 c[x]의 합
//sum_d[i]는 루트를 i로 하는 트리에 대해 c[x] * d(i, x)의 합
vector<llint> sub_sum_c(n), sub_sum_d(n);
auto dfs
=[&](auto &&self, int v, int par) -> pair<llint, llint> {
//v: 현재 노드, par: 부모 노드
for (int t: tree[v]) { //모든 하위방향 노드들에 대해
if (t == par) continue; //부모 방향으로는 가지 않는다
auto [child_sum_c, child_sum_d] = self(self, t, v);
sub_sum_c[v] += child_sum_c; //하위방향 c를 누적
sub_sum_d[v] += child_sum_d; //하위방향 d를 누적
}
sub_sum_d[v] += sub_sum_c[v]; //재귀적으로 c[x]가 d(i, x)번 합해진다
sub_sum_c[v] += c[v];
return {sub_sum_c[v], sub_sum_d[v]};
}; dfs(dfs, 0, -1); //루트에서부터 dfs, 0(1)번 노드를 루트로 취급
//dfs를 통해 모든 노드에 대해 f(n)을 구합니다.
vector<llint> f(n);
auto reroot
=[&](auto &&self, int v, int par, llint par_sum_c, llint par_sum_d) -> void {
//v: 현재 노드, par: 부모 노드, par_sum_c: 상위방향으로의 c합, par_sum_d: 상위방향으로의 d합
f[v] = sub_sum_d[v] + par_sum_d;
for(int t : tree[v]) { //모든 하위방향 노드들에 대해
if(t == par) continue; //부모 방향으로는 가지 않는다
llint nc = par_sum_c //v의 상위방향으로의 c 합
+ sub_sum_c[v] //v의 하위방향으로의 c합
//여기까지 모든 노드의 c합
- sub_sum_c[t]; //t의 하위방향으로의 c합 뺀다
//nc : t의 상위방향으로의 c합
llint nd = par_sum_d //v의 상위 방향으로의 d합
+ sub_sum_d[v] //v의 하위방향으로의 d합
- sub_sum_d[t] - sub_sum_c[t] //t의 양방향 d합을 뺸다
//여기까지 t가 v위치에 있었을 때 sum_d
+ nc; //t의 상위방향으로의 c합
//nd : t의 상위방향으로의 d합
self(self, t, v, nc, nd);
}
}; reroot(reroot, 0, -1, 0, 0);
cout << *min_element(f.begin(), f.end()) << endl;
}